아두이노 - 도트 매트릭스 제어하기, dot matrix

2019. 10. 22. 20:12

아두이노에 8 x 8 도트 매트릭스를 연결하고 제어해보자.

도트 매트릭스를 사용하여 하트 캐릭터와 HELLO WORLD 문자를 한 글자씩 표시해보고 더 나아가 LED 전광판처럼 HELLO WORLD 전체 문자열이 오른쪽에서 왼쪽으로 이동하면서 표시되도록 코딩해보자.

예제에 사용되는 부속들은 알리익스프레스에서 구매한 "최신 RFID 스타터 키트, Arduino UNO R3 업그레이드 버전 - improved version"을 구매하여 사용하였습니다. 사용된 구성품을 확인하실 수 있습니다.

NEWEST RFID Starter Kit for Arduino UNO R3 Upgraded version Learning Suite With Retail Box - AliExpress 502

Smarter Shopping, Better Living! Aliexpress.com

www.aliexpress.com

연결

아두이노 2 번핀 -> 도트 매트릭스 9 번핀

아두이노 3 번핀 -> 도트 매트릭스 10 번핀

아두이노 4 번핀 -> 도트 매트릭스 11 번핀

아두이노 5 번핀 -> 도트 매트릭스 12 번핀

아두이노 6 번핀 -> 도트 매트릭스 13 번핀

아두이노 7 번핀 -> 도트 매트릭스 14 번핀

아두이노 8 번핀 -> 도트 매트릭스 15 번핀

아두이노 9 번핀 -> 도트 매트릭스 16 번핀

아두이노 A5(19) 번핀 -> 도트 매트릭스 8 번핀

아두이노 A4(18) 번핀 -> 도트 매트릭스 7 번핀

아두이노 A3(17) 번핀 -> 도트 매트릭스 6 번핀

아두이노 A2(16) 번핀 -> 도트 매트릭스 5 번핀

아두이노 10 번핀 -> 도트 매트릭스 4 번핀

아두이노 11 번핀 -> 도트 매트릭스 3 번핀

아두이노 12 번핀 -> 도트 매트릭스 2 번핀

아두이노 13 번핀 -> 도트 매트릭스 1 번핀

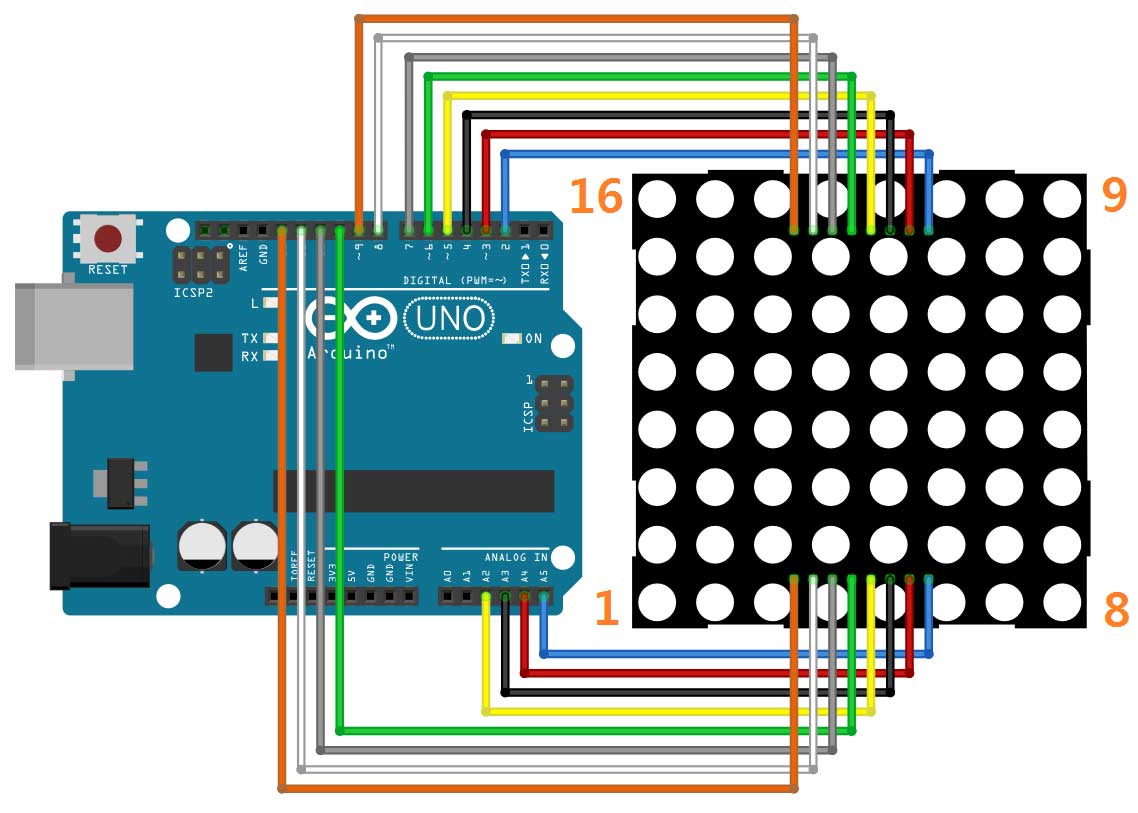
아두이노 - 도트 매트릭스 연결, 사진의 원안처럼 돌기가 나와있는 곳이 도트 매트릭스 전면부이고 왼쪽부터 핀번호1 ~ 8이다.

도트 매트릭스의 핀 부위에 돌기가 나와 있는 면이 전면이다. 전면을 기준으로 왼쪽 핀부터 핀번호 1 ~ 8번이고 위쪽으로 이동해서 우측부터 9번 ~ 16번 순으로 가게 된다. 상기 연결도를 참조하여 연결을 해보자.

도트 매트릭스 제어 코드를 살펴보기에 앞서 아래 기초 이론을 알아야 이해하기 쉽다.

LED: 발광 다이오드

전류: 두 전극 사이의 전위차에 의해 발생하는 흐름(5V - 0V : 전위차 5 발생, 전류는 5V -> 0V로 흐른다)

다이오드의 특성: 순방향으로 전류가 흐를 때 저항이 작고 역방향으로 전류가 흐를 때는 저항이 크다.

아래 그림의 LED는 순방향으로는 전류가 잘 흐르지만, 역방향은 전류가 거의 흐르지 않게 된다.

애노드(anode): 전류가 들어가는 전극, 양극

캐소드(cathode): 전류가 나오는 전극, 음극

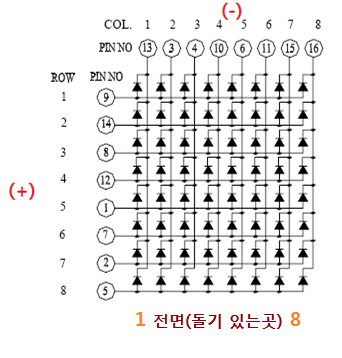
도트 매트릭스 보는 방법

전면부를 아래로 하고 위에서 내려다봤을 때(상기 우측 그림) 위쪽이 1행(ROW1), 아래쪽이(돌기 있는 곳) 8행(ROW8)이고 왼쪽이 1열(COL1), 오른쪽이 8열(COL8)이다.

상기 그림에서 1행을 제어하기 위해서는 핀번호 9번을 제어를 해야 하고 8행을 제어하기 위해서는 핀번호 5번을 제어해야 한다. 마찬가지로 1열을 제어하기 위해서는 핀번호 13번, 8열을 제어하기 위해서는 핀번호 16번을 제어해야 한다. 만약 1행 1열을 제어하고 싶다면 핀번호 9번과 13번을 제어하면 된다.

여기서 살펴보아야 할게 상기 왼쪽 그림의 순방향에 따른 기호표를 살펴보고 오른쪽 그림의 기호표와 비교해보자. 행을 제어하는 모든 핀은 LED의 애노드에 연결되어 있고 열을 제어하는 모든 핀은 LED의 캐소드에 연결되어 있느것을 확인할 수 있다. 즉 애노드에 5V(HIGH)를 주고 캐소드에 0V(LOW)를 주게 되면 애노드와 캐소드 사이에 전위차가 발생하여 전류가 흐르게 되고 LED는 발광하게 된다. 여기서 다시 캐소드에 5V(HIGH)를 주게 되면 양단에 5V가 걸리게 되어 전위차가 0이 되므로 전류는 흐르지 않게 되고 LED는 발광하지 않는다. 만약 행을 제어하는 핀에 0V를 주고 열을 제어하는 핀에 5V를 주게 되면 전위차가 5 발생하지만 역방향 전류가 발생하게 된다. 역방향 전류는 거의 흐르지 않는 다이오드의 특성상 전류가 흐르지 않게 되어 이때에도 LED는 발광하지 않게 된다. 간단하게 얘기하자면 행과 열을 제어하는 핀에 상시 5V(HIGH)를 걸어주고(LED가 꺼진 상태) 열을 제어하는 핀에 필요에 따라 0V(LOW)로 변경해 주어 LED를 켜고 끄는 제어를 할 수 있게 된다.

더 자세히 살펴보자.

9번 핀에 5V를 걸어주면 1행 8개 LED에 5V가 걸리게 된다. 이때 13번 핀에 0V를 걸어주면 1행 1열의 LED가 켜지고 다시 5V를 걸어주면 LED가 꺼지게 된다. 또한 3번 핀에 0V 걸어주면 1행 2열의 LED가 켜지고 5V를 걸어주면 LED가 꺼지는 방식으로 1열 전체를 제어할 수 있게 된다.

이제 아두이노의 핀번호와 도트 매트릭스의 핀번호를 매칭 시켜보자.

도트 매트릭스의 행을 제어하기 위해 8비트 자료형 rowPin[8] 배열을 선언해주고 {1행-9, 2행-14, .... 8행-5}에 맞도록 연결도의 핀번호를 기입해준다.

연결도에서 1행을 제어하는 도트 매트릭스의 9번 핀에 연결된 것은 파란색 아두이노 2번 핀이다.

2행을 제어하는 토트 매트릭스의 14번 핀에 연결된 것은 회색 아두이노 7번 핀이다.

3행을 제어하는 토트 매트릭스의 8번 핀에 연결된 것은 회색 아두이노 19(A5)번 핀이다.

8행을 제어하는 도트 매트릭스의 5번 핀에 연결된 것은 노란색 아두이노 16(A2)번 핀이다.

상기 내용을 배열로 표현하면 아래와 같다.

uint8_t rowPin[8] = {2, 7, 19, 5, 13, 18, 12, 16}; // {1행-9, 2행-14, 3행-8, 4행-12, 5행-1, 6행-7, 7행-2, 8행-5}

열의 배열도 상기와 같은 방식으로 표현하면 아래와 같다.

uint8_t colPin[8] = {6, 11, 10, 3, 17, 4, 8, 9};

도트 매트릭스를 사용하는 데 있어서 가장 혼란스럽게 만드는 핀 연결 및 핀번호 매칭이 완료되었다. 이제 아두이노의 기본 예제를 살펴보고 도트 매트릭스의 좌표 한 개부터 시작하여 열 단위, 행 단위를 제어해 보자.

좌표 한 개 제어

/* 아두이노 - 도트 매트릭스 핀 연결
byte rowPin[8] = {2, 7, 19, 5, 13, 18, 12, 16};  // {1행, 2행, 3행, 4행, 5행, 6행, 7행, 8행}
byte colPin[8] = {6, 11, 10, 3, 17, 4, 8, 9}; // {1열, 2열, 3열, 4열, 5열, 6열, 7열, 8열}
*/

#define row 2  // 행 제어 핀번호
#define col 9 // 열제어 핀번호

void setup() {
  pinMode(row, OUTPUT);  // 행 제어 핀 출력 설정
  pinMode(col, OUTPUT); // 열제어 핀 출력 설정
  digitalWrite(row, HIGH); // row 핀 제어 - 1행 전원 공급
}

void loop() {
  digitalWrite(col, LOW);   // col핀 제어-1열 전원 차단 -> 0V -> 전위차 발생 -> 전류 흐름, LED ON
  delay(1000);
  digitalWrite(col, HIGH);  // col핀 제어-1열 전원 공급 -> 5V -> 전위차 없음 -> 전류 흐르지 않음, LED OFF
  delay(1000);
}

arduino_dot_matrix_x_y_control.ino

0.00MB

코딩한 코드를 아두이노에 업로드하면 1행 8열의 도트가 점멸하는 것을 볼 수 있다.

#define row 2의 핀 번호 2를 원하는 행 번호에 맞게 변경해주고 #define col 9의 핀번호 9를 열 번호에 맞게 변경해주면 해당 좌표의 도트가 점멸하도록 제어할 수 있다. 아두이노와 도트 매트릭스의 모든 핀이 연결된 상태이지만 상기 코드에서는 행과 열의 제어 출력 핀을 한 개씩만 핀 모드에서 설정해 주었으므로 전체 도트를 제어하지 못하고 한 좌표만 제어를 하게 된다.

아두이노에 연결된 모든 핀을 핀 모드에서 OUTPUT으로 설정해주고 전체 도트를 제어해보자

for 루프를 사용하여 미리 정의된 행과 열 배열의 모든 핀을 OUTPUT으로 설정해준다.

for (int i = 0; i < 8; i++) {
pinMode(rowPin[i], OUTPUT); // 모든 행 제어 핀 모드 OUTPUT 설정
pinMode(colPin[i], OUTPUT); // 모든 열 제어 핀 모드 OUTPUT 설정
}

특정 행 제어 핀에 500 밀리초 간격으로 5V(HIGH), 0V(LOW)를 주어 5V가 걸려있을 때에는 열 제어 핀의 상태 값에 따라 도트의 LED가 켜지고 꺼질 수 있도록 준비상태를 부여하고 0V가 걸려 있을 때에는 열 제어 핀의 상태 값에 상관없이 특정 행의 모든 도트가 OFF 상태가 되어 리프레시 상태(다음 상태 값을 켜기 위한 준비)가 되도록 해준다.

  for (int i = 0; i < 8; i++) {  // 행 제어 핀 전체 켜고 끄기
    digitalWrite(rowPin[i], HIGH);  // 모든 행 제어 핀에 전원 공급, LED ON 준비(열 제어 핀 상태에 따라 ON)
    delay(500);                     // 전원 공급 상태 유지 시간
    digitalWrite(rowPin[i], LOW);   // 모든 행 제어 핀에 전원 차단, 열 제어 핀 상태에 상관없이 OFF)
  }

열의 상태를 제어하기 위해 변수 byte pattern = 0b11111111;를 설정해주고 아래와 같이 입력값을 갖는 사용자 함수를 설정하여 setonoff(pattern); 형식으로 pattern값을 적용하도록 해준다.

void setonoff(byte state) {     // 입력값을 갖는 사용자 함수
  for(int i = 0; i < 8; i++) {  // 8개 열의 상태 값을 pattern 변수에서 추출
    bool a = state >> i & 0x01? LOW : HIGH; // bool 자료형 사용 변숫값 변경 비트 마스크
    digitalWrite(colPin[i], a); // 열 제어 핀 0b11111111 비트 값에 맞게 설정
  }
}

변수 pattern에서 열의 비트 상태 값을 추출하기 위해 삼항 연산자를 이용하는 비트 마스크를 사용하였다. 비트 마스크에 대해 자세히 알고 싶다면 이전 글 아두이노 - 비트 마스크, bit mask를 참조하길 바란다.

dot_matrix_row_control.ino

0.00MB

byte rowPin[8] = {2, 7, 19, 5, 13, 18, 12, 16};  // {1행, 2행, 3행, 4행, 5행, 6행, 7행, 8행}
byte colPin[8] = {6, 11, 10, 3, 17, 4, 8, 9};    // {1열, 2열, 3열, 4열, 5열, 6열, 7열, 8열} 

byte pattern = 0b11111111;      // 8개 열의 상태값 정의

void setup() {
  for (int i = 0; i < 8; i++) {
    pinMode(rowPin[i], OUTPUT); // 모든 행 제어 핀모드 OUTPUT 설정 
    pinMode(colPin[i], OUTPUT); // 모든 열 제어 핀모드 OUTPUT 설정 
  }
}

void loop() {  
  setonoff(pattern);                // 8개 열의 상태값을 pattern 변수에서 추출한뒤 설정하는 사용자 함수
  for (int i = 0; i < 8; i++) {     // delay(500); 시간 간격으로 아래로 한칸씩 행 이동행 제어핀 전체 켜고 끄기
    digitalWrite(rowPin[i], HIGH);  // 해당 행 제어핀에 전원공급, LED ON 준비(열 제어핀 상태에 따라 ON)
    delay(500);                     // 전원공급 상태 유지 시간
    digitalWrite(rowPin[i], LOW);   // 해당 행 제어핀에 전원차단, 열 제어핀 상태에 상관없이 OFF)
  }
}

void setonoff(byte state) {     // 입력값을 갖는 사용자 함수
  for(int i = 0; i < 8; i++) {  // 8개 열의 상태값을 pattern 변수에서 추출  
    bool a = state >> i & 0x01? LOW : HIGH; // bool 자료형 사용 변수값 변경 비트 마스크
    digitalWrite(colPin[i], a); // 열 제어핀 0b11111111 비트값에 맞게 설정 
  }
}

상기 코드를 업로드하면 "0b11111111"의 상태 값에 따라 1열이 모두 켜진 상태에서 delay(500); 시간 간격에 따라 행이 위에서 아래로 변경되는 것을 확인할 수 있다. 여기에서 열의 상태 값인 이진수 "0b11111111"을 다른 값으로 변경해주면(0b11101011, 0b11111000...) 그 비트 값을 반영하여 표시되는 것을 볼 수 있다. 즉, 아래 그림처럼 1행의 8개 열을 모두 출력하고 다음 2행의 8개 열, .... 8행의 8개 열을 출력하는 것을 반복하게 된다. 반복하는 주기가 빠르게 되면 전체 8개행 모든 도트가 동시에 작동하는 것처럼 느끼게 될 것이다.

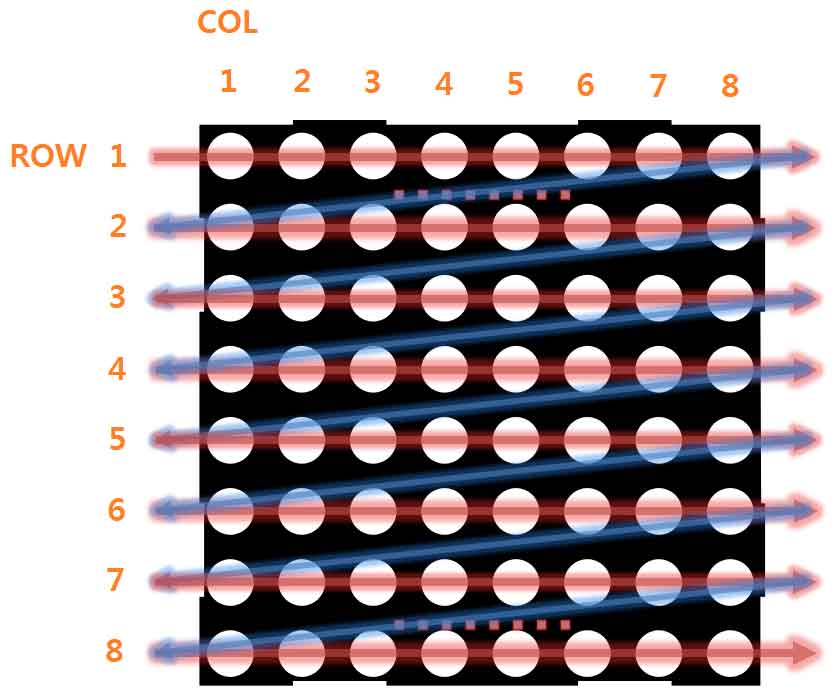
배열을 이용하여 행이 바뀌는 것에 따라 열의 상태 값 또한 바뀌도록 변경해 보자.

byte pattern = 0b11111111; 변수를 8개의 배열로 변경해주고 각 배열 요소에 이진수 상태 값을 아래와 같이 입력해준다.

byte pattern[8] = {0b01000010,0b10100101,0b10011001,0b10000001,0b10000001,0b01000010,0b00100100,0b00011000};

loop() 함수의 행 변경 for() 루프 코드 내에 행 변경 인자인 "i" 값에 연동하도록 setonoff(pattern[i]);와 같이 열 변경 함수를 위치시키게 되면 행이 위에서 아래로 변경될 때마다 행 번호에 해당하는 열 상태 값이 반영되어 도트 매트릭스에 표시되는 것을 볼 수 있다.

dot_matrix_row_col_control.ino

0.00MB

byte rowPin[8] = {2, 7, 19, 5, 13, 18, 12, 16};  // {1행, 2행, 3행, 4행, 5행, 6행, 7행, 8행}
byte colPin[8] = {6, 11, 10, 3, 17, 4, 8, 9};    // {1열, 2열, 3열, 4열, 5열, 6열, 7열, 8열} 

byte pattern[8] = {0b01000010,0b10100101,0b10011001,0b10000001,0b10000001,0b01000010,0b00100100,0b00011000};

void setup() {
 for (int i = 0; i < 8; i++) {
  pinMode(rowPin[i], OUTPUT); // 모든 행 제어 핀모드 OUTPUT 설정 
  pinMode(colPin[i], OUTPUT); // 모든 열 제어 핀모드 OUTPUT 설정 
 }
}

void loop() {   
  for (int i = 0; i < 8; i++) {     // delay(500); 시간 간격으로 아래로 한칸씩 행 이동행 제어핀 전체 켜고 끄기
    setonoff(pattern[i]);           // 8개 열의 상태값을 pattern 변수에서 추출한뒤 설정하는 사용자 함수
    digitalWrite(rowPin[i], HIGH);  // 해당 행 제어핀에 전원공급, LED ON 준비(열 제어핀 상태에 따라 ON)
    delay(500);                     // 전원공급 상태 유지 시간
    digitalWrite(rowPin[i], LOW);   // 해당 행 제어핀에 전원차단, 열 제어핀 상태에 상관없이 OFF)
  }
}

void setonoff(byte state) {    
  for(int i = 0; i < 8; i++) {  // 8개 열의 상태값을 pattern 변수에서 추출  
    bool a = state >> i & 0x01? LOW : HIGH; // bool 자료형 사용 변수값 변경 비트 마스크
    digitalWrite(colPin[i], a); // 열 제어핀 0b11111111 비트값에 맞게 설정 
  }
}

상기 코드에서 delay(500);을 delay(1);로 변경하고 업로드하면 빠르게 각 행마다 열 값을 쓰게 되어 눈으로 보기에는 정지된 하트 문자처럼 보이게 된다.

아두이노 기본 예제를 살표 보자.

아두이노 IDE에서 파일 -> 예제 -> Display -> RowColumnScanning 스케치를 불러오면 가변저항 두 개를 연결하여 X축(열)과 Y축(행)을 제어하도록 코드가 제시되어 있다. 또한 아두이노와 도트 매트릭스를 연결방법을 제시하는 글이 있는 아두이노 참조 사이트를 확인할 수 있다.

이 예제에서 가변저항 대신 시리얼 모니터에서 X, Y값을 입력하여 제어하도록 해보자. 아래와 같이 가변저항 관련 코드를 시리얼 모니터 제어용 코드로 코딩해 주었다.

// 가변저항 제어 코드
x = 7 - map(analogRead(A0), 0, 1023, 0, 7);
y = map(analogRead(A1), 0, 1023, 0, 7);

// 시리얼 모니터 제어 코드
if (Serial.available() > 0) {  // read the sensors for X and Y values:
  String temp = Serial.readStringUntil('\n');
  if (temp.indexOf(",") != -1) {
    String x_temp = temp.substring(0, temp.indexOf(","));
    String y_temp = temp.substring(temp.indexOf(",") + 1, temp.length());
    x = x_temp.toInt();
    y = y_temp.toInt();
  }
}

또한 예제 코드에서는 좌표값이 변동될 경우를 대비해서 loop() 함수가 스캔할 때마다 현재 도트를 끄도록 하기 위해 pixels[x][y] = HIGH; 코드를 사용하였으나 이는 좌표 값의 변동이 없을 때에도 매 스캔마다 무조건 꺼졌다 켜지도록 하고 있다. 물론 꺼지고 켜지는 시간이 극히 짧아 눈으로 인지할 수는 없다. 이를 시리얼 모니터에 의해 좌표값이 전송될 때에만 현재 도트를 끄도록 위치를 조정해 주었다.

dot_matrix_example.ino

0.00MB

const int row[8] = {2, 7, 19, 5, 13, 18, 12, 16};
const int col[8] = {6, 11, 10, 3, 17, 4, 8, 9};

int pixels[8][8]; // 좌표값 이차원 배열 선언

int x = 4; // x, y 좌표 초기값 -> 6행, 6열
int y = 4;

void setup() {
  Serial.begin(9600);
  for (int thisPin = 0; thisPin < 8; thisPin++) {  
    pinMode(col[thisPin], OUTPUT);    
    pinMode(row[thisPin], OUTPUT);
    digitalWrite(col[thisPin], HIGH);  // 열 제어핀에 5V(HIGH)를 주어 확실하게 토트가 OFF 되도록 함
  }
  for (int x = 0; x < 8; x++) {    // 이차원배열 모든 좌표값을 HIGH 로 초기화
    for (int y = 0; y < 8; y++) {  // refreshScreen() 함수에 의해
      pixels[x][y] = HIGH;         // 열 상태 값은 HIGH로 변경됨
    }
  }
}

void loop() {
  readSensors();    // 좌표 값 읽기
  refreshScreen();  // 좌표 값 쓰기
}

void readSensors() {  
  if (Serial.available() > 0) {  // x, y 좌표값 읽기
    String temp = Serial.readStringUntil('\n');
    if (temp.indexOf(",") != -1) {
      pixels[x][y] = HIGH;  // 새 좌표값을 읽기 전에 이전 좌표의 도트 끄기
      String x_temp = temp.substring(0, temp.indexOf(","));
      String y_temp = temp.substring(temp.indexOf(",") + 1, temp.length());
      x = x_temp.toInt();
      y = y_temp.toInt();
    }
  }
  pixels[x][y] = LOW; // 이차원배열 인데스 x,y에 LOW값 입력, refreshScreen() 함수에 의해 
}                     // y열의 상태 값 LOW, 해당 도트 켜짐

void refreshScreen() {
  for (int x = 0; x < 8; x++) {    // 8개 행 제어 
    digitalWrite(row[x], HIGH);    // 한개 행 5V 걸어서 열 상태값에 따라 켜지고 꺼지도록 준비
    for (int y = 0; y < 8; y++) {  // 8개 열 제어
      int thisPixel = pixels[x][y]; // 현재 행열 상태값 HIGH 또는 LOW 저장
      digitalWrite(col[y], thisPixel); // 현재 열 제어핀에 상태값 쓰기 - 열 전체 도트 영향 받음
      if (thisPixel == LOW) {          // 만약 현재 열에 LOW 값이 있으면 다음행으로 넘어갈 때 꺼진상태를 유지하기위해 
        digitalWrite(col[y], HIGH);    // 현재 열이 꺼지도록 초기화 한다.
      }
    }
    digitalWrite(row[x], LOW);    // 현재 행에 0V를 주어 다음 행 제어시 영향을 받지 않도록 한다.  
  }
}

상기 코드를 업로드하고 시리얼 모니터에서 전송 옵션을 "새 글"로 한 상태에서 "0,0"을 입력하면 1행 1열 도트가 켜지고 "6,6"을 입력하면 7행 7열, "2,5"입력하면 3행 6열의 도트가 켜지는 것을 볼 수 있다.

핵심 코드 분석

void refreshScreen() {
  for (int x = 0; x < 8; x++) {    // 8개 행 제어
    digitalWrite(row[x], HIGH);    // 한 개 행 5V 걸어서 열 상태 값에 따라 켜지고 꺼지도록 준비
    for (int y = 0; y < 8; y++) {  // 8개 열 제어
      int thisPixel = pixels[x][y]; // 현재 행열 상태 값 HIGH 또는 LOW 저장
      digitalWrite(col[y], thisPixel); // 현재 열 제어 핀에 상태 값 쓰기 - 열 전체 도트 영향 받음
      if (thisPixel == LOW) { // 만약 현재 열에 LOW 값이 있으면 다음행으로 넘어갈 때 꺼진 상태를 유지하기 위해
        digitalWrite(col[y], HIGH);    // 현재 열을 모두 다시 꺼지도록 초기화한다.
      }
    }
    digitalWrite(row[x], LOW);    // 행 값을 끈다.
  }
}

상기 코드는 아래 행 제어 코드에 따라 행이 변경될 때마다 해당 행에 HIGH를 주어 열제어 코드의 상태 값에 따라 도트 가 켜지고 꺼지도록 준비하고 열제어 코드의 실행이 완료되면 다시 LOW로 변경하여 다음 열을 제어할 때 영향을 받지 않도록 해준다.

for (int x = 0; x < 8; x++) { // 행 제어 코드
  digitalWrite(row[x], HIGH);  // 행에 5V를 걸어주어 토트를 켤 준비를 한다.
  열 제어 코드
  digitalWrite(row[x], LOW);    // 행에 0V를 주어 다음 행 제어 시 영향을 받지 않도록 한다.
}

해당 행에 HIGH인 상태에서 아래 열제어 코드에 따라 열의 상태 값을 한 개씩 확인하고 써준다.

for (int y = 0; y < 8; y++) {  // 8개 열 제어
  int thisPixel = pixels[x][y]; // 현재 행열 상태 값 HIGH 또는 LOW 저장
  digitalWrite(col[y], thisPixel);
}

이 코드에서 만약 좌표 5, 5가 LOW였다면 digitalWrite(col[5], LOW); 가 되어 6행 6열의 도트에 불이 들어오게 된다. 즉 초기값 HIGH에서 현재 상태 값 LOW로 변경되어 토트가 켜지게 되는 것이다. 위 코드처럼 LOW인 상태에서 코드가 종료된다면 행 제어 코드에 의해 다음 행으로 넘어갈 때 digitalWrite(col[5], LOW); 인 상태로 들어가게 되어 7행 6열의 도트에도 불이 들어온 상태로 진입한 뒤 현재 상태 값 HIGH를 반영한 뒤에야 digitalWrite(col[5], HIGH);가 되어 도트가 꺼지게 된다. 즉 초기값이 LOW인 상태에서 진입한 뒤 현재 상태 값 HIGH로 변경되어 꺼지게 되는 것이다. 이를 방지하기 위해 아래 코드가 포함되어야만 픽셀 하나만 제어를 할 수 있다. 상기 스케치에서 아래 코드를 주석 처리해보고 확인해 보자.

if (thisPixel == LOW) { // 만약 현재 열에 LOW 값이 있으면
digitalWrite(col[y], HIGH); // 현재 열을 모두 다시 꺼서 좌표의 도트만 잠깐 켜지도록 한다.
}

도트 매트릭스에 HELLO WORLD 한 글자씩 표시해 보자.

아래 사이트에서 코드를 참조하고 이전 예제 코드를 적용하였다.

http://www.86duino.com/?p=8300

dot_matrix_hello_world.ino

0.00MB

//여러 줄을 묶은 매크로 '\' 이용, '\' 뒤에 어떤것도 없어야됨
#define SPACE { \
    {0, 0, 0, 0, 0, 0, 0, 0}, \
    {0, 0, 0, 0, 0, 0, 0, 0}, \
    {0, 0, 0, 0, 0, 0, 0, 0}, \
    {0, 0, 0, 0, 0, 0, 0, 0}, \
    {0, 0, 0, 0, 0, 0, 0, 0}, \
    {0, 0, 0, 0, 0, 0, 0, 0}, \
    {0, 0, 0, 0, 0, 0, 0, 0}, \
    {0, 0, 0, 0, 0, 0, 0, 0} \
}
#define H { \
    {0, 1, 0, 0, 0, 0, 1, 0}, \
    {0, 1, 0, 0, 0, 0, 1, 0}, \
    {0, 1, 0, 0, 0, 0, 1, 0}, \
    {0, 1, 1, 1, 1, 1, 1, 0}, \
    {0, 1, 0, 0, 0, 0, 1, 0}, \
    {0, 1, 0, 0, 0, 0, 1, 0}, \
    {0, 1, 0, 0, 0, 0, 1, 0}, \
    {0, 1, 0, 0, 0, 0, 1, 0}  \
}
#define E  { \
    {0, 1, 1, 1, 1, 1, 1, 0}, \
    {0, 1, 0, 0, 0, 0, 0, 0}, \
    {0, 1, 0, 0, 0, 0, 0, 0}, \
    {0, 1, 1, 1, 1, 1, 1, 0}, \
    {0, 1, 0, 0, 0, 0, 0, 0}, \
    {0, 1, 0, 0, 0, 0, 0, 0}, \
    {0, 1, 0, 0, 0, 0, 0, 0}, \
    {0, 1, 1, 1, 1, 1, 1, 0}  \
}
#define L { \
    {0, 1, 0, 0, 0, 0, 0, 0}, \
    {0, 1, 0, 0, 0, 0, 0, 0}, \
    {0, 1, 0, 0, 0, 0, 0, 0}, \
    {0, 1, 0, 0, 0, 0, 0, 0}, \
    {0, 1, 0, 0, 0, 0, 0, 0}, \
    {0, 1, 0, 0, 0, 0, 0, 0}, \
    {0, 1, 0, 0, 0, 0, 0, 0}, \
    {0, 1, 1, 1, 1, 1, 1, 0}  \
}
#define O { \
    {0, 0, 0, 1, 1, 0, 0, 0}, \
    {0, 0, 1, 0, 0, 1, 0, 0}, \
    {0, 1, 0, 0, 0, 0, 1, 0}, \
    {0, 1, 0, 0, 0, 0, 1, 0}, \
    {0, 1, 0, 0, 0, 0, 1, 0}, \
    {0, 1, 0, 0, 0, 0, 1, 0}, \
    {0, 0, 1, 0, 0, 1, 0, 0}, \
    {0, 0, 0, 1, 1, 0, 0, 0}  \
}
#define W { \
    {1, 0, 0, 0, 0, 0, 0, 1},\
    {1, 0, 0, 0, 0, 0, 1, 0},\
    {1, 0, 0, 0, 0, 0, 1, 0},\
    {0, 1, 0, 1, 0, 0, 1, 0},\
    {0, 1, 0, 1, 0, 1, 0, 0},\
    {0, 1, 0, 1, 0, 1, 0, 0},\
    {0, 0, 1, 1, 0, 1, 0, 0},\
    {0, 0, 0, 1, 1, 0, 0, 0},\
}
#define R { \
    {1, 1, 1, 1, 1, 0, 0, 0},\
    {1, 0, 0, 0, 1, 0, 0, 0},\
    {1, 0, 0, 0, 1, 0, 0, 0},\
    {1, 1, 1, 1, 1, 0, 0, 0},\
    {1, 0, 1, 0, 0, 0, 0, 0},\
    {1, 0, 0, 1, 0, 0, 0, 0},\
    {1, 0, 0, 0, 1, 0, 0, 0},\
    {1, 0, 0, 0, 0, 1, 0, 0},\
}
#define D { \
    {1, 1, 1, 1, 1, 0, 0, 0},\
    {1, 1, 0, 0, 1, 1, 0, 0},\
    {1, 1, 0, 0, 0, 1, 1, 0},\
    {1, 1, 0, 0, 0, 1, 1, 0},\
    {1, 1, 0, 0, 0, 1, 1, 0},\
    {1, 1, 0, 0, 0, 1, 1, 0},\
    {1, 1, 0, 0, 1, 1, 0, 0},\
    {1, 1, 1, 1, 1, 0, 0, 0},\
}

byte rowPin[8] = {2, 7, 19, 5, 13, 18, 12, 16};  // {1행, 2행, 3행, 4행, 5행, 6행, 7행, 8행}
byte colPin[8] = {6, 11, 10, 3, 17, 4, 8, 9};    // {1열, 2열, 3열, 4열, 5열, 6열, 7열, 8열} 

const int numPatterns = 11;  //표현할 글자 수
unsigned long startTime = 0;

byte patterns[numPatterns][8][8] = {  //표현할 문자 패턴, numPatterns 의 갯수에 맞게 표시
  H,E,L,L,O,W,O,R,L,D,SPACE      //H,E,L,L,O,SPACE
};
                   
void setup() {
 for (byte i = 0; i < 8; i++) {
  pinMode(rowPin[i], OUTPUT);
  pinMode(colPin[i], OUTPUT);
 }
}

void loop() {
  setonoff();
}

void setonoff() { 
  for (byte i = 0; i < numPatterns; i++,  startTime = millis()) { // 1초후 단어간 이동, 시간 초기화
    while (millis() - startTime < 900) {  // 1초 동안 문자 표시
      for (byte j = 0; j < 8; j++) { // row 위치 조정
        for (byte k =0; k < 8; k++) { // col 위치 조정
          boolean a = !patterns[i][j][k]; // 3차원 배열값 가져오기
          digitalWrite(colPin[k], a); // col 핀 제어
        }
        digitalWrite(rowPin[j], HIGH); // row 핀 제어
        delay(1);
        digitalWrite(rowPin[j], LOW);
      }
    }
    delay(100); // 단어간 구분 - 껏다 킴
  }
}

핵심 코드 분석

byte patterns[numPatterns][8][8] = { //표현할 문자 패턴, numPatterns의 개수에 맞게 표시
H,E,L,L,O,W,O,R,L,D,SPACE //H,E,L,L,O,SPACE
};

3차원 배열을 정의하는 데에 있어 2차원 배열 매크로를 사용하였다.

3차원 배열은 코딩할 때 다음과 같이 높이(또는 층의 수)x가로x세로 형태이로 이루어지고 아래와 같이 정의한다.

자료형 배열 이름[높이 또는 층의 수][면의 행 크기][면의 열 크기];

int numArr[2][3][4] = {
    { { 11, 22, 33, 44 }, { 55, 66, 77, 88 }, { 99, 110, 121, 132 } },
    { { 111, 122, 133, 144 }, { 155, 166, 177, 188 }, { 199, 1110, 1121, 1132 } }
};

// 3차원 배열에 값 저장 및 읽기
numArr[1][1][2] = 0;        // 2층의 2번째 배열에서 인덱스 2번에 값 저장 177 -> 0
int temp = numArr[0][1][2]  // 1층의 2번째 배열에서 인덱스 2번의 값 일고 대입 -> 77

상기 코드의 면에 해당하는 2차원 배열 요소 { { 11, 22, 33, 44 }, { 55, 66, 77, 88 }, { 99, 110, 121, 132 } }를 매크로를 이용하여 문자형태(H,E,L,L,O.... )로 정의하였다. 정의된 각 문자의 자리에 2차원 배열이 치환되게 된다.

#define H { \
    {0, 1, 0, 0, 0, 0, 1, 0}, \
    {0, 1, 0, 0, 0, 0, 1, 0}, \
    {0, 1, 0, 0, 0, 0, 1, 0}, \
    {0, 1, 1, 1, 1, 1, 1, 0}, \
    {0, 1, 0, 0, 0, 0, 1, 0}, \
    {0, 1, 0, 0, 0, 0, 1, 0}, \
    {0, 1, 0, 0, 0, 0, 1, 0}, \
    {0, 1, 0, 0, 0, 0, 1, 0}  \
}
// 한 줄로 표현하면 아래와 같다.
#define H { {0, 1, 0, 0, 0, 0, 1, 0}, {0, 1, 0, 0, 0, 0, 1, 0}, {0, 1, 0, 0, 0, 0, 1, 0}, {0, 1, 1, 1, 1, 1, 1, 0}, {0, 1, 0, 0, 0, 0, 1, 0},
{0, 1, 0, 0, 0, 0, 1, 0}, {0, 1, 0, 0, 0, 0, 1, 0}, {0, 1, 0, 0, 0, 0, 1, 0} }

상기 코드에서는 여러 줄을 묶어서 매크로로 정의하는 방법을 사용했다.
#define은 줄 바꿈이 일어날 때 \를 사용하여 여러 줄을 매크로로 만들 수 있다. 단, 맨 마지막 줄은 \를 사용하지 않아도 된다.

#define 매크로 이름 코드 1 \
코드 2 \
코드 3

따라서 마지막 줄 } 다음에는 \ 표시가 없다.

void setonoff() {
  for (byte i = 0; i < numPatterns; i++,  startTime = millis()) { // 1초 후 단어 간 이동, 시간 초기화
    while (millis() - startTime < 900) {  // 1초 동안 문자 표시
      for (byte j = 0; j < 8; j++) { // row 위치 조정
        for (byte k =0; k < 8; k++) { // col 위치 조정
          boolean a = !patterns[i][j][k]; // 3차원 배열 값 가져오기
          digitalWrite(colPin[k], a); // col 핀 제어
        }
        digitalWrite(rowPin[j], HIGH); // row 핀 제어
        delay(1);
        digitalWrite(rowPin[j], LOW);
      }
    }
    delay(100); // 단어 간 구분 - 껐다 킴
  }
}

for 루프에서 조건을 만족하면 두 가지 연산을 실행하도록 되어 있다. i를 증가시키는 증감 연산(i++)과 밀리 초를 변수에 저장하는 대입 연산(startTime = millis())을 실행한다. for 루프 시작과 동시에 저장된 millis() 값에 지속되는 while 루프가 900 밀리 초동 안 소요하고 while루프를 빠져나오면 delay(100); 동안 더 소요되어 약 1초 뒤에 for 루프의 i값이 증가하게 된다.

그 1초의 시간 사이에 while 루프에 의해 900 밀리초 동안 도트 매트릭스에 3차원 배열의 층수에 해당하는 문자의 배열을 출력하고 delay(100);에 의해 모든 도트 매트릭스를 끔으로써 단어 간 구분을 하게 된다.

delay(100); 코드를 삭제하거나 delay(1);로 변경하면 부드럽게 단어가 변경이 되나 LL처럼 연속되는 같은 단어의 구분이 되지 않게 된다. 필요에 따라 수정하면 된다.

HELLO WORLD 문자열을 오른쪽에서 왼쪽으로 이동하여 표시되게 해 보자.

이전 코드에서는 각 문자(3차원 인덱스의 높이, 또는 층)를 기준으로 한 글자씩 출력해 주었다. 하지만 문자열의 이동을 표시하기 위해서는 문자 간 겹치는 구간이 생기게 되는데 이를 코딩할 때 코드로 구현해 주어야 한다.

문자열이 이동한다는 것은 3차원 배열 "patterns[i][j][k]"의 최초 1행 ~8행의 1회 출력(한문자 또는 3차원 인덱스 높이)하면 'H' 문자가 표시되고 그다음 1개 열이 이동하면 'H' 문자의 1열은 사라지고 다음 문자인 'E' 문자의 1열이 추가로 붙게 된다. 아래 그림처럼 'H' 문자와 'E'문자가 합쳐진 새로운 문자가 생성되고 이러한 작업이 총 문자수가 11개라면 한문자 당 이동 열 개수는 8이므로 11 x 8 = 88개가 되고, 이는 11개 문자의 문자열이 이동을 완료하는 3차원 배열의 높이 인덱스가 되게 된다. 즉, "8 x 8" 면 배열이 88개(높이 또는 층)가 있고 이 배열이 일정 시간 간격으로 도트 매트릭스에 표시되면 문자열이 이동하는 효과가 나타나게 되는 것이다.

88개의 이차원 배열을 만들고 그 배열을 일정 간격으로 도트 매트릭스에 표시해 주어도 문자열이 이동하게 되지만 88개의 이차원 배열을 만드는 것 자체도 문제일 뿐만 아니라 문자가 바뀔 때마다 새로 전체 배열을 만들어 줘야 된다는 문제가 있게 된다.

상기 그림을 참조하여 새로운 문자가 생성될 때의 인덱스 변화 패턴을 분석하여 패턴을 표현하는 코드를 작성해 주면 새로운 배열을 생성하지 않고 문자에 대한 배열만을 이용하여 문자열이 이동하는 표현을 할 수 있게 된다.

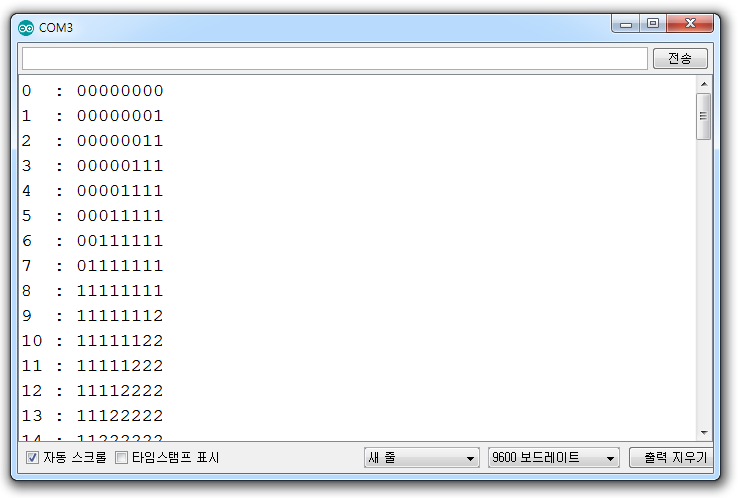
88개의 층이 하나씩 증가할 때마다 인덱스 i값의 변화를 살펴보면 0층에서는 1행 ~ 8행의 1회 출력되는 동안 8개 열의 i값은 00000000(오랜지색 1행)이다. 출력이 완료되면 한 칸 왼쪽으로 이동하게 되는데 이때가 두 번째 층이 출력되는 부분이다. 이 층의 8개 열의 i값을 살펴보면 00000001(파란색 1행)이 된다. 이렇게 층이 증가할수록 i값의 위치가 한 칸씩 왼쪽으로 이동하다 8개 층의 출력이 완료되면 11111111이 되고 다음 층이 완료되면 11111112 이런 식으로 8개 층을 기준으로 문자 인덱스 숫자가 바뀌며 층수가 증가할수록 왼쪽으로 이동하게 된다. 좀 더 단순화시키면 아래와 같다.

0,0,0,0,0,0,0,0. 1,1,1,1,1,1,1,1, 2,2,2,2,2,2,2,2, ~ 11,11,11,11,11,11,11,11

상기 숫자 배열이 있고 8개 칸이 있는 필터를 한 칸씩 우측으로 이동시켜서 보는 것과 같은 것이다.

이를 코드로 표현하면 아래와 같다.

  for (byte i = 0; i <= (patterns * 8); i++) {
    for (byte k = 0; k < 8; k++) {
      byte val = (i + k) / 8;
}
}

상기 코드에서 변수 i는 3차원 인덱스의 층수이고 k는 8개 칸의 필터가 된다(8개 묶음)

층수가 0일 때 val = 00000000

층수가 1일 때 val = 00000001

층수가 2일 때 val = 00000011

아래 스케치를 업로드하고 출력되는 값을 확인해 보자.

cubic_array_i_cal.ino

0.00MB

void setup() {
  Serial.begin(9600);
  byte patterns = 12; 
  for (byte i = 0; i <= (patterns * 8); i++) { 
    Serial.print(i); 
    if (i < 10) Serial.print("  : ");
    else Serial.print(" : ");
    for (byte k = 0; k < 8; k++) {
      byte val = (i + k) / 8;
      Serial.print(val);
    }
    Serial.println();
  }
}

void loop() {
}

상기의 방법을 적용하여 이제 인덱스 k값의 변화를 살펴보자.

층수가 0일 때 val = 01234567

층수가 1일 때 val = 12345670

층수가 2일 때 val = 23456701 이 되어 층수가 증가할 때마다 0 ~ 7의 숫자가 한 칸씩 이동하면서 루프 하고 있다. 이를 코드로 표현하면 아래와 같다.

for (byte i = 0; i <= (patterns * 8); i++) { // 글자 수 당 8열
    for (byte k = 0; k < 8; k++) {
      byte val = (i+k) % 8;
    }
}

아래 스케치를 업로드하고 출력되는 값을 확인해 보자.

array_k_index_loop.ino

0.00MB

void setup() {
  Serial.begin(9600);
  byte patterns = 12;  //표현할 글자 수
  for (byte i = 0; i <= (patterns * 8); i++) { // 글자수당 8열
    Serial.print(i); 
    if (i < 10) Serial.print("  : ");
    else Serial.print(" : ");
    for (byte k = 0; k < 8; k++) {  
      byte val = (i+k) % 8;
      Serial.print(val);
    }
    Serial.println();
  }
}

void loop() {
}

왼쪽으로 슬라이드 될 때에는 처음 시작이 SPACE부터 시작해야 'H'문자의 1열이 토트 매트릭스의 8열에서 나오기 시작한다. 따라서 SPACE 문자를 문자열 앞에 추가해 준다.

const int numPatterns = 12;  //표현할 글자 수
byte patterns[numPatterns][8][8] = {  //표현할 문자 패턴, numPatterns의 개수에 맞게 표시
  SPACE,H,E,L,L,O,W,O,R,L,D,SPACE      //H,E,L,L,O,SPACE
};

이전에 HELLO WORLD를 한 글자씩 출력했던 코드에 상기에서 구현한 3차원 인덱스 변화 코드를 적용시켜보면 아래와 같다.

void setonoff() {
  for (byte i = 0; i <= (numPatterns-1) * 8 ; i++,  startTime = millis()) { // 전체 칸수, 시간 초기화
    while (millis() - startTime < 60) {  // 한 칸 이동 시간
      for (byte j = 0; j < 8; j++) { // row 위치 조정
        for (byte k =0; k < 8; k++) { // col 위치 조정
          boolean a = !patterns[(i+k)/8][j][(i+k)%8]; // (i+k)/8: 열 한칸씩 이동, (i+k)%8: 이동만큼 열 위치 회전
          digitalWrite(colPin[k], a); // col 핀 제어
        }
      digitalWrite(rowPin[j], HIGH); // row 핀 제어
      delay(1);
      digitalWrite(rowPin[j], LOW);
      }
    }
  }
}

한문자씩 출력할 때에는 for 루프 변수 i가 문자수와 같았었지만 텍스트 이동 코드에서는 열 이동에 따른 새로 생성되는 층수가 포함된 숫자(문자수 x 8)로 변경해줘야 된다. 스페이스를 포함해서 문자수는 12개 이고 마지막 문자가 SPACE이다 하지만 실제 출력하고자 하는 문자는 11개가 되게 된다. 마지막 문자 SPACE 문자의 열까지 계속해서 열을 이동시킨다면 다음 13번째 문자가 있어야 되는데 13번째 문자는 없다. 따라서 전체 출력 열 개수는 12 x 8 = 96개가 아닌 11 x 8 = 88개가 된다. 즉 1개 문자는 공백이라고 보면 된다. 이를 적용한 코드는 "(numPatterns-1) * 8"이다. 또한 900 밀리초 동안 한 문자 출력이 유지되던 것을 1열 이동하는 시간에 맞게 밀리 초값을 조절해 주어야 한다.

아래 스케치를 업로드하고 밀리초 값을 변경해 텍스트 이동 속도를 조절해 보자.

dot_matrix_hello_world_slide_left.ino

0.00MB

//여러 줄을 묶은 매크로 '\' 이용, '\' 뒤에 어떤것도 없어야됨, 표현할 문자를 2진수로 정의 새로운 문자 추가 가능.
#define SPACE { \
    {0, 0, 0, 0, 0, 0, 0, 0}, \
    {0, 0, 0, 0, 0, 0, 0, 0}, \
    {0, 0, 0, 0, 0, 0, 0, 0}, \
    {0, 0, 0, 0, 0, 0, 0, 0}, \
    {0, 0, 0, 0, 0, 0, 0, 0}, \
    {0, 0, 0, 0, 0, 0, 0, 0}, \
    {0, 0, 0, 0, 0, 0, 0, 0}, \
    {0, 0, 0, 0, 0, 0, 0, 0}, \
}
#define H { \
    {0, 1, 0, 0, 0, 0, 1, 0}, \
    {0, 1, 0, 0, 0, 0, 1, 0}, \
    {0, 1, 0, 0, 0, 0, 1, 0}, \
    {0, 1, 1, 1, 1, 1, 1, 0}, \
    {0, 1, 0, 0, 0, 0, 1, 0}, \
    {0, 1, 0, 0, 0, 0, 1, 0}, \
    {0, 1, 0, 0, 0, 0, 1, 0}, \
    {0, 1, 0, 0, 0, 0, 1, 0}  \
}
#define E  { \
    {0, 1, 1, 1, 1, 1, 1, 0}, \
    {0, 1, 0, 0, 0, 0, 0, 0}, \
    {0, 1, 0, 0, 0, 0, 0, 0}, \
    {0, 1, 1, 1, 1, 1, 1, 0}, \
    {0, 1, 0, 0, 0, 0, 0, 0}, \
    {0, 1, 0, 0, 0, 0, 0, 0}, \
    {0, 1, 0, 0, 0, 0, 0, 0}, \
    {0, 1, 1, 1, 1, 1, 1, 0}  \
}
#define L { \
    {0, 1, 0, 0, 0, 0, 0, 0}, \
    {0, 1, 0, 0, 0, 0, 0, 0}, \
    {0, 1, 0, 0, 0, 0, 0, 0}, \
    {0, 1, 0, 0, 0, 0, 0, 0}, \
    {0, 1, 0, 0, 0, 0, 0, 0}, \
    {0, 1, 0, 0, 0, 0, 0, 0}, \
    {0, 1, 0, 0, 0, 0, 0, 0}, \
    {0, 1, 1, 1, 1, 1, 1, 0}  \
}
#define O { \
    {0, 0, 0, 1, 1, 0, 0, 0},\
    {0, 0, 1, 0, 0, 1, 0, 0},\
    {0, 1, 0, 0, 0, 0, 1, 0},\
    {0, 1, 0, 0, 0, 0, 1, 0},\
    {0, 1, 0, 0, 0, 0, 1, 0},\
    {0, 1, 0, 0, 0, 0, 1, 0},\
    {0, 0, 1, 0, 0, 1, 0, 0},\
    {0, 0, 0, 1, 1, 0, 0, 0},\
}
#define W { \
    {1, 0, 0, 0, 0, 0, 0, 1},\
    {1, 0, 0, 0, 0, 0, 1, 0},\
    {1, 0, 0, 0, 0, 0, 1, 0},\
    {0, 1, 0, 1, 0, 0, 1, 0},\
    {0, 1, 0, 1, 0, 1, 0, 0},\
    {0, 1, 0, 1, 0, 1, 0, 0},\
    {0, 0, 1, 1, 0, 1, 0, 0},\
    {0, 0, 0, 1, 1, 0, 0, 0},\
}
#define R { \
    {1, 1, 1, 1, 1, 0, 0, 0},\
    {1, 0, 0, 0, 1, 0, 0, 0},\
    {1, 0, 0, 0, 1, 0, 0, 0},\
    {1, 1, 1, 1, 1, 0, 0, 0},\
    {1, 0, 1, 0, 0, 0, 0, 0},\
    {1, 0, 0, 1, 0, 0, 0, 0},\
    {1, 0, 0, 0, 1, 0, 0, 0},\
    {1, 0, 0, 0, 0, 1, 0, 0},\
}
#define D { \
    {1, 1, 1, 1, 1, 0, 0, 0},\
    {1, 1, 0, 0, 1, 1, 0, 0},\
    {1, 1, 0, 0, 0, 1, 1, 0},\
    {1, 1, 0, 0, 0, 1, 1, 0},\
    {1, 1, 0, 0, 0, 1, 1, 0},\
    {1, 1, 0, 0, 0, 1, 1, 0},\
    {1, 1, 0, 0, 1, 1, 0, 0},\
    {1, 1, 1, 1, 1, 0, 0, 0},\
}

byte rowPin[8] = {2, 7, 19, 5, 13, 18, 12, 16};  // {1행, 2행, 3행, 4행, 5행, 6행, 7행, 8행}
byte colPin[8] = {6, 11, 10, 3, 17, 4, 8, 9};    // {1열, 2열, 3열, 4열, 5열, 6열, 7열, 8열} 

unsigned long startTime = 0;

const int numPatterns = 12;  //표현할 글자 수
byte patterns[numPatterns][8][8] = {  //표현할 문자 패턴, numPatterns 의 갯수에 맞게 표시
  SPACE,H,E,L,L,O,W,O,R,L,D,SPACE      //H,E,L,L,O,SPACE
};
                   
void setup() {
  for (byte i = 0; i < 8; i++) {
    pinMode(rowPin[i], OUTPUT);
    pinMode(colPin[i], OUTPUT);
  }
}

void loop() {
  setonoff();
}

void setonoff() { 
  for (byte i = 0; i <= (numPatterns-1) * 8 ; i++,  startTime = millis()) { // 전체 칸수, 시간 초기화
    while (millis() - startTime < 60) {  // 한칸 이동 시간
      for (byte j = 0; j < 8; j++) { // row 위치 조정
        for (byte k =0; k < 8; k++) { // col 위치 조정
          boolean a = !patterns[(i+k)/8][j][(i+k)%8]; // (i+k)/8: 열 한칸씩 이동, (i+k)%8: 이동만큼 열위치 회전
          digitalWrite(colPin[k], a); // col 핀 제어
        }
      digitalWrite(rowPin[j], HIGH); // row 핀 제어
      delay(1);
      digitalWrite(rowPin[j], LOW);
      }
    }
  }
}

[arduino] - 아두이노 - 비트 연산자

[arduino] - 아두이노 - 비트 시프트 연산자

[arduino] - 아두이노 - 비트 마스크, bit mask

[arduino] - 아두이노 - 도트 매트릭스 제어하기, dot matrix

저작자표시 비영리 변경금지

'Arduino' 카테고리의 다른 글

ESP8266 / ESP32 - HTTPClient.h 라이브러리 이용 날씨 정보 받기, RSS / API (4)	2019.11.04
아두이노 - ESP01 모듈, 기상청 / 오픈웨더맵 API 날씨 정보 받기 (18)	2019.11.03
아두이노 IDE 환경 설정하기 - preferences.txt 설정, 에디터 폰트 변경(추천) (0)	2019.10.31
ESP8266 / ESP32 - time.h 라이브러리 이용 시간 출력 및 NTP 서버 시간 동기화 하기 (0)	2019.10.28
아두이노 - 비트 마스크, bit mask (0)	2019.10.19
아두이노 - 비트 시프트 연산자 (0)	2019.10.16
아두이노 - 비트 연산자 (0)	2019.10.16
아두이노 우노와 NodeMcu의 성능 비교, MCU 속도 벤치 마크 (0)	2019.10.16

postpop

아두이노 - 도트 매트릭스 제어하기, dot matrix

'Arduino' 카테고리의 다른 글

+ Recent posts

티스토리툴바